Exercise Set 7
BUDGET CONSTRAINT
I. Objectives
- To sketch the budget constraint, given prices and income
- To understand how changes in price and income affect the budget constraint
II. Data
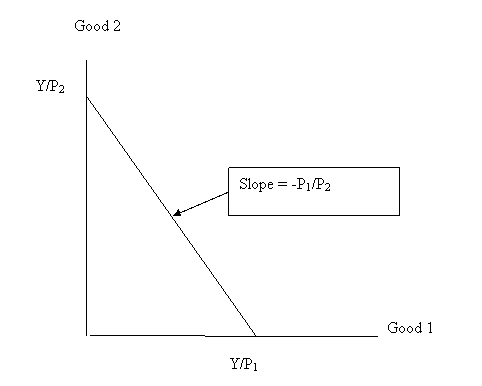
- The equation for the budget constraint is P1Q1 + P2Q2 = Y, where P1 is the price of Good 1, P2 is the price of Good 2, Q1 is the quantity of Good 1, Q2 is the quantity of Good 2, and Y is the consumer's income.
- Choose values for the parameters (prices and income).
- Sketch the budget constraint. Indicate the intercepts and slope. [Plot Good 1 (Q1) on the horizontal axis.]
Click on Gimme Budget Constraint! to confirm your calculations.
III. Questions
Given: The price of a unit of Good 1 is $20. The price of a unit of Good 2 is $5. The consumer's
income is $100.
- Sketch the budget constraint (with Q1 on the horizontal axis). Indicate the intercepts and slope.
Note: Verify that the slope equals -P1/P2.
- "An increase in P1 will cause the horizontal intercept to rise and the budget constraint to rotate outwards." Anything wrong with the statement? Provide a sketch.
- Go back to the original prices and income. Suppose income falls by 10%. What is the effect
on the intercepts and slope of the budget constraint? Provide a sketch of the old and new constraints.
- Go back to the original prices and income. If the price of Good 2 falls by 20%, ceteris paribus, what will happen to the intercepts and slope of the budget constraint? Sketch the old and new constraints.
IV. Additional questions
- Newt Gingrich consumes nachos and milk. The slope of his budget constraint is -4. We may infer that
- The ratio of Newt's income to the price of nachos is 4
- The ratio of the prices of the two goods is 4
- The slope of the budget constraint will increase as he moves down the budget constraint
- Both (a) and (c) are true
- None of the above is true
- An increase in the price of a good, ceteris paribus, causes
- The budget constraint to rotate inward, i.e. toward the origin
- The budget constraint to rotate outward, i.e. away from the origin
- The budget constraint to shift outward, i.e. away from the origin
- The budget constraint to shift inward, i.e. toward the origin
- You spend 5 hours every evening watching TV and studying for your classes. Denoting the number of hours spent on TV by NT and the number of hours spent on studies by NS, sketch the "budget constraint" that you face every evening. Which of the following is true about the slope of this constraint?
- The slope is -1/5
- The slope is -1
- The magnitude of the slope equals the opportunity cost (measured in hours) of watching TV
- The magnitude of the slope equals the opportunity cost (measured in hours) of studying
- The choices (b), (c) and (d) are correct
- Both (a) and (c) are correct
- A decrease in the price of a good, ceteris paribus, causes
- The budget constraint to rotate inward, i.e. toward the origin
- The budget constraint to rotate outward, i.e. away from the origin
- The budget constraint to shift outward, i.e. away from the origin
- The budget constraint to shift inward, i.e. toward the origin
- A decrease in the consumer's income, ceteris paribus, will lead to
- Higher consumption of goods if they are normal goods
- Lower consumption of goods if they are normal goods
- An outward and parallel shift of the budget constraint
- An inward rotation of the budget constraint
- Both (a) and (d)
- The magnitude of the slope of the budget constraint
- Is the ratio of prices of two goods
- Is the ratio of income to price of a good
- Falls as we move down the budget constraint
- Is always the same as the marginal rate of substitution
- None of the above
- Sly Stallone consumes peanuts and wine. The price of peanuts is $2 per pound; that of wine is $10 per gallon; and his income is $400. If you sketch the budget constraint with peanuts on the horizontal axis, which of the following is true?
- The horizontal intercept is 200
- The horizontal intercept is 40
- The vertical intercept is 800
- The slope is -5
- Both (a) and (d)
Answers to selected questions:
1b 2a 3e 4b 5b
6a 7a
Home
