Exercise Set 7.5
Duopoly

Two firms compete in a market. Demand is given by p = a - b(q + Q), where p is price, q is Firm A's output, and Q is Firm B's output. Firm A's marginal cost is c, Firm B's is C. Each firm has a fixed cost of f.

Suppose a = 800, b = 2, c = 440, C = 500, f = 10.

1. Write Firm A's and Firm B's profit functions.
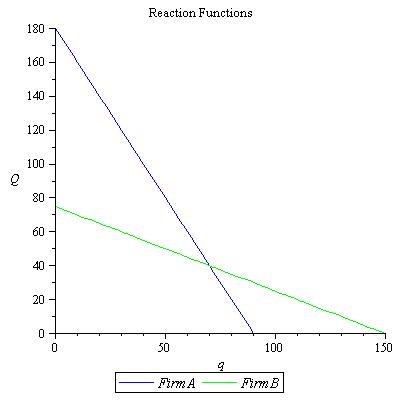
2. Obtain Firm A's reaction function. Sketch it, with Q on the vertical axis. Indicate the intercepts and slope.
3. Obtain Firm B's reaction function and sketch it. Indicate the intercepts and slope.
4. Solve for the optimal values of q and Q. (This is the Nash equilibrium.)
5. Obtain the price charged by both firms.
6. Compute each firm's profits. Is B's profit smaller or larger than A's? Explain.
7. If c increases, ceteris paribus, will Firm A produce more output or less? How about Firm B? Will the total output in the market increase or decrease? Will the price go up or down?
8. Show the results of the increase in c on the reaction functions and the Nash equilibrium.

Answers: The initial Nash equilibrium occurs at q = 70, Q = 40. Firm B will make profits of 3190.