min C = 3x + 4y
s.t. 3x - 4y ≤ 12,
x + 2y ≥ 4,
x ≥ 1, y ≥ 0.
Steps
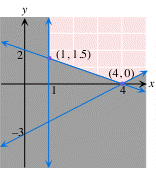
min C = 3x + 4y
s.t. 3x - 4y ≤ 12,
x + 2y ≥ 4,
x ≥ 1, y ≥ 0.

| Point | Objective function: C = 3x + 4y |
| (1,1.5) | 9 |
| (4,0) | 12 |
Example 2
A farmer plants wheat and rye on his 10 acres of land. He has to plant at least 7 acres. He has $1,200 to spend. An acre of wheat costs $200 to plant while an acre of rye costs $100. The farmer has to get the planting done in 12 hours. It takes an hour to plant an acre of wheat and 2 hours to plant an acre of rye. If the profit is $500 per acre of wheat and $300 per acre of rye, how many acres of each should the farmer plant in order to maximize profits? [Source]
Obtain the constraints and plot them. In the figure below, acres of wheat is on the horizontal axis.
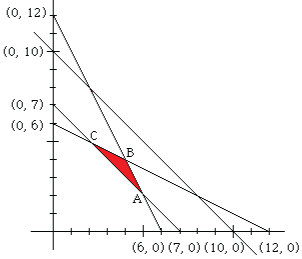
Corner points of the feasible region: